Table Of Content
For instance, in the design depicted in Table 1, the effect of Extended Medication would be reflected by the average effect of all Extended Medication conditions (1–16) versus the average effect of all Standard Medication conditions (17–32). With effect coding, when the experimental conditions have equal (or nearly equal) numbers of participants, the main effect of a factor does not reflect the effects of interaction effects that may be present in the data. Recall that in a simple between-subjects design, each participant is tested in only one condition.
Types of Factorial Design
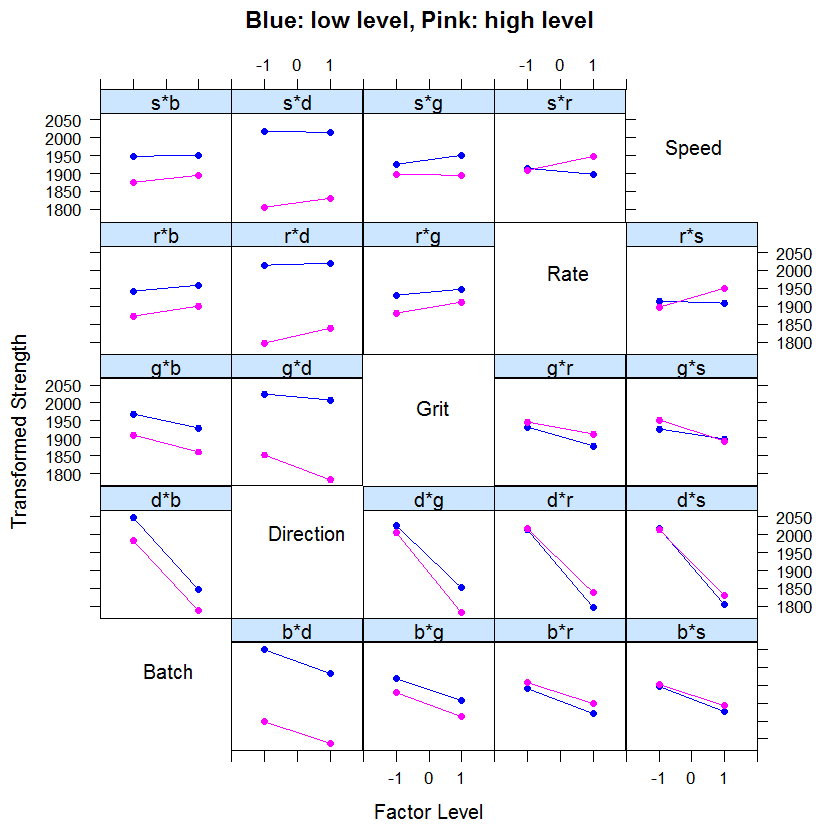
The factors that have significant effects are shown in red and the ones without significant effects are shown in black. The further a factor is from the blue line, the more significant effect it has on the corresponding response. For wt% methanol in biodiesel, RPM is further from the blue line than pressure, which indicates that RPM has a more significant effect on wt% methanol in biodiesel than pressure does. The Pareto charts show which factors have statistically significant effects on the responses. As seen in the above plots, RPM has significant effects for both responses and pressure has a statistically significant effect on wt% methanol in biodiesel. Neither flow rate or ratio have statistically significant effects on either response.
Establishing a conceptual model and understanding optimization
When taking a general linear model approach to the analysis of data from RCTs and factorial experiments, analysts must decide how to code categorical independent variables. This problem is avoided if an analysis of variance package is used, because such packages typically default to effect coding. However, as noted by Kugler et al. (Kugler, Trail, Dziak, & Collins, 2012), in regression analyses investigators may use either dummy coding (also known as reference cell coding) or effect coding (also known as unweighted effects coding) (cf. Cohen, Cohen, West, & Aiken, 2003). In dummy coding, a binary variable, a reference group (e.g., a control group) is assigned a value of zero (0) and the other group (e.g., an active treatment group) is assigned a value of one (1). Effect coding of a binary variable is the same except that the zero for the reference group is replaced with −1. In many factorial designs, one of the independent variables is a non-manipulated independent variable.
Main Effects
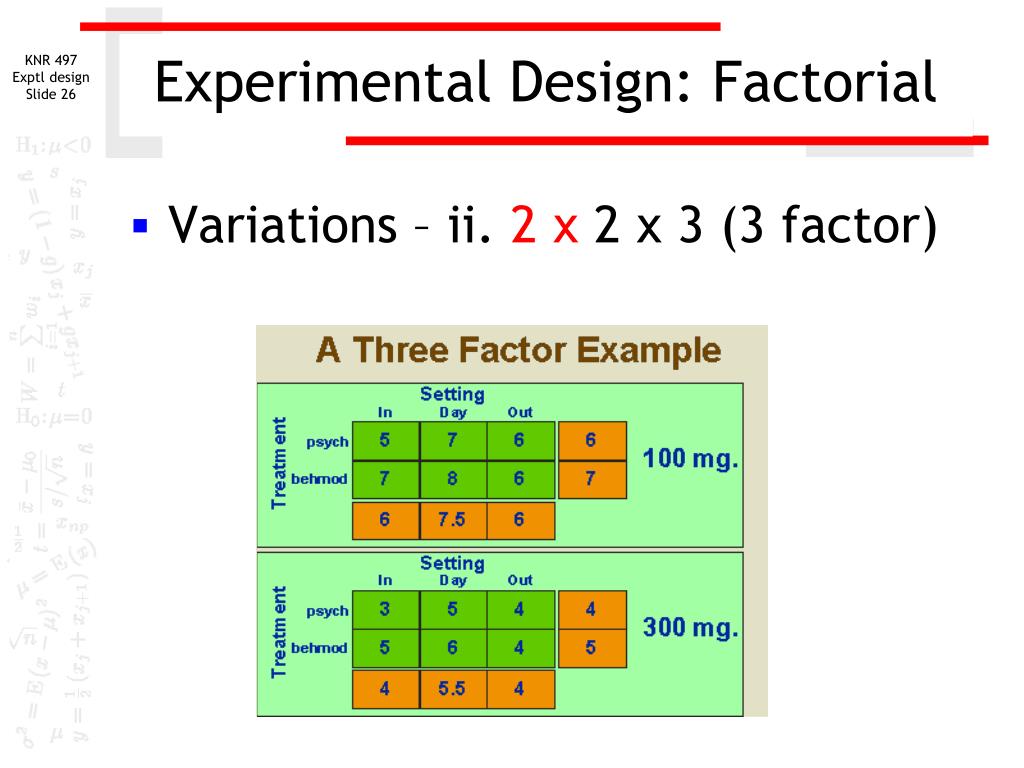
A contrast in cell means is a linear combination of cell means in which the coefficients sum to 0. Contrasts are of interest in themselves, and are the building blocks by which main effects and interactions are defined. The expected response to a given treatment combination is called a cell mean,[12] usually denoted using the Greek letter μ. (The term cell is borrowed from its use in tables of data.) This notation is illustrated here for the 2 × 3 experiment. Other terms for "treatment combinations" are often used, such as runs (of an experiment), points (viewing the combinations as vertices of a graph, and cells (arising as intersections of rows and columns). Experimental design also allows researchers to generalize their findings to the larger population from which the sample was drawn.
For example, the levels of an 6-level factor might simply be denoted 1, 2, ..., 6. If the number of combinations in a full factorial design is too high to be logistically feasible, a fractional factorial design may be done, in which some of the possible combinations (usually at least half) are omitted. This paper presents the application of an advanced quality management tool, the design of experiments (DOE), in order to characterise a new material (carbon fibre-reinforced polyamide) used in the 3D printing process. The study focuses on the definition of optimal 3D printing parameters, such as nozzle size, temperature, print speed, layer height and print orientation, to achieve desired mechanical properties. The results show that layer height and print orientation have a significant effect on mechanical properties and printing time.
For example, a researcher might choose to treat cell phone use as a within-subjects factor by testing the same participants both while using a cell phone and while not using a cell phone (while counterbalancing the order of these two conditions). But he or she might choose to treat time of day as a between-subjects factor by testing each participant either during the day or during the night (perhaps because this only requires them to come in for testing once). Observing the effects of at least two independent variables is a more practical and economical approach. This averts the need to expend time and resources for separate experiments. Furthermore, collecting data for different combinations of conditions enables researchers to make a variety of assessments, including main and interaction effects. This scientific approach is designated a label that either underscores the number of factors or the number of conditions tested for each independent variable.
This method can be used to capture detailed information about participants’ behavior or to analyze social interactions. Behavioral measures involve measuring participants’ behavior directly, such as through reaction time tasks or performance tests. These measures may be administered using specialized equipment or software. This design involves grouping participants within larger units, such as schools or households, and then randomly assigning these units to different treatment groups.
Screening autism-associated environmental factors in differentiating human neural progenitors with fractional factorial ... - Nature.com
Screening autism-associated environmental factors in differentiating human neural progenitors with fractional factorial ....
Posted: Thu, 29 Jun 2023 07:00:00 GMT [source]
Data Analysis Method
One Factor at a Time and factorial experimental design for formulation of l-carnitine microcapsules to improve its ... - ScienceDirect.com
One Factor at a Time and factorial experimental design for formulation of l-carnitine microcapsules to improve its ....
Posted: Mon, 15 Jan 2024 08:00:00 GMT [source]
They are simple to design and analyze, while providing information that can be used to inform more detailed follow-up experiments using only the factors found to be important. More details on full and fractional factorial designs can be found in ref. 4. We can apply the same reasoning in a 26 experiment to remove half the runs. In the 32-run 26–1 fractional factorial design there are 32 confounding relations (e.g., ABCDEF with the intercept, A with BCDEF, etc.), and, importantly, all of the main effects and two-factor interactions are confounded with four- and five-factor interactions. Given our assumption that these high-order effects are unlikely to be important, we have little worry that they will contaminate our estimate of the main effects and two-factor interactions. Higher order interactions can reflect complex patterns that defy easy interpretation.
Differences between factorial experiments and RCTs
For instance, while a real world application of a treatment might involve the administration of only two bundled ICs (counseling + medication), a factorial experiment might involve 6 or more ICs. Such effects would be manifest in interactions amongst components (e.g., the effectiveness of a component might be reduced when it is paired with other components) or in increased data missingness. Moreover, if higher order interactions are not examined in models, researchers will not know if an intervention component is intrinsically weak (or strong) or is meaningfully affected by negative (or positive) interactions with other factors. In general, if the major goal of a study is to contrast directly one “treatment” with another treatment (e.g., a control treatment), then an RCT is usually the best choice.
In keeping with this, the data in Figure 1 suggest that we can winnow potentially promising combinations from 16, to 3. Which one of those three might be deemed most promising might be addressed via other criteria (effects on abstinence, costs, and so on) and in a follow-up RCT. Thus, two different active treatments might be contrasted with one another in a two-group design, such as a comparison of two different counseling approaches (e.g., skill training vs. supportive counseling), each paired with the same medication. Neither one of these conditions would be a control condition in a strict sense, since each delivers a different form of active treatment. In addition, an RCT might have a control condition, but this might be used in comparisons with many active treatment conditions. For instance, in the comparative treatment design, multiple active treatment conditions are contrasted with a single common control condition (e.g., each of four conditions might receive a different active medication, and each is then compared with a single placebo condition).
Two-level factorial experiments, in which all combinations of multiple factor levels are used, efficiently estimate factor effects and detect interactions—desirable statistical qualities that can provide deep insight into a system. This gives them an edge over the widely used one-factor-at-a-time experimental approach, which is statistically inefficient and unable to detect interactions because it sequentially varies each factor individually while all the others are held constant. It is important to note that interpretation of complex higher order interactions may not be aided by simple effects testing. First, it is highly unlikely that such testing would have distinguished amongst the three leading combinations shown in Figure 1 (the differences in outcomes are too small).
Moreover, especially in complex designs, the coded levels such as the low- and high-level of a factor are easier to understand. For the vast majority of factorial experiments, each factor has only two levels. For example, with two factors each taking two levels, a factorial experiment would have four treatment combinations in total, and is usually called a 2×2 factorial design.
Also notice that each number in the notation represents one factor, one independent variable. So by looking at how many numbers are in the notation, you can determine how many independent variables there are in the experiment. 2 x 2, 3 x 3, and 2 x 3 designs all have two numbers in the notation and therefore all have two independent variables.
Just as it is common for studies in education (or social sciences in general) to include multiple levels of a single independent variable (new teaching method, old teaching method), it is also common for them to include multiple independent variables. As we will see, interactions are often among the most interesting results in empirical research. A factorial design is a type of experiment that involves manipulating two or more variables. While simple psychology experiments look at how one independent variable affects one dependent variable, researchers often want to know more about the effects of multiple independent variables.

No comments:
Post a Comment